Approach
-
Overview
Learning Problem
Feedback Net Architecture
GAN Architecture
1. Overview
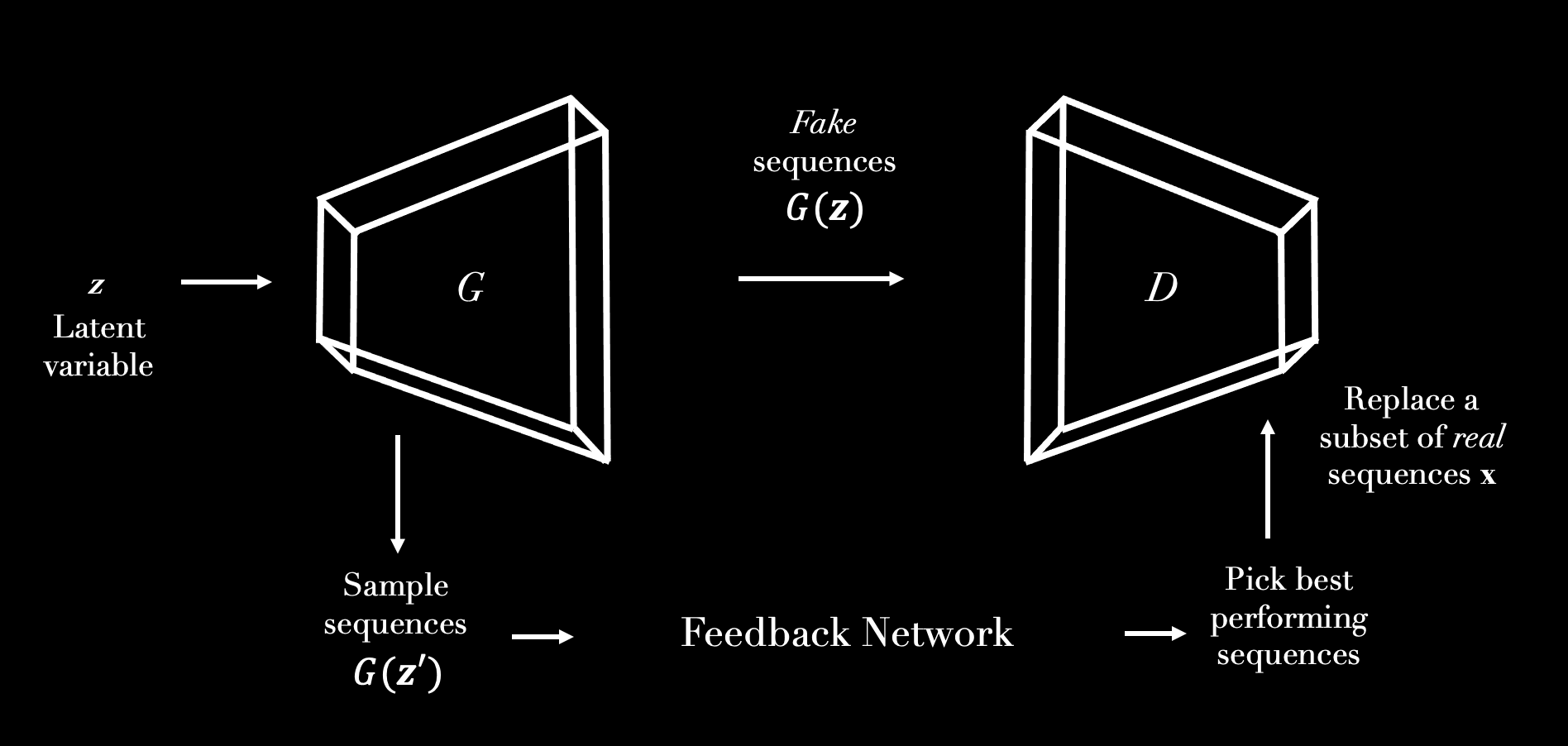 Generative Adversarial Networks (GANs) learn patterns and structures from the real data and harnesses
this information to create novel data (Goodfellow et al., 2014) .
We have used a Generative Adversarial Network coupled with Feedback Network
to produce novel protein sequences optimized to contain specific 3D structural properties.
This implements and extends the feedback loop mechanism desrcibed by Gupta et al. 2019.
Generative Adversarial Networks (GANs) learn patterns and structures from the real data and harnesses
this information to create novel data (Goodfellow et al., 2014) .
We have used a Generative Adversarial Network coupled with Feedback Network
to produce novel protein sequences optimized to contain specific 3D structural properties.
This implements and extends the feedback loop mechanism desrcibed by Gupta et al. 2019.
Our approach is:
- Train GAN to produce realistically looking sequences.
-
Train Feedback Net to recognize presence of 8 structural features in protein sequences.
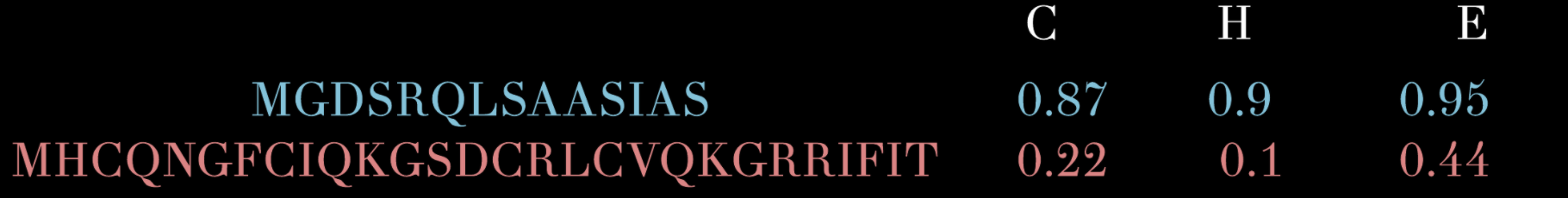
- Pass the sequences produced by the Generator the the Feedback Net and score them.
-
If all desired structural properties in the generated sequences pass a pre-set treshold score,
add them to the real training set of the Discriminator.
Continue until the Generator learns important patterns of the top-scoring sequences and produces desired
features.
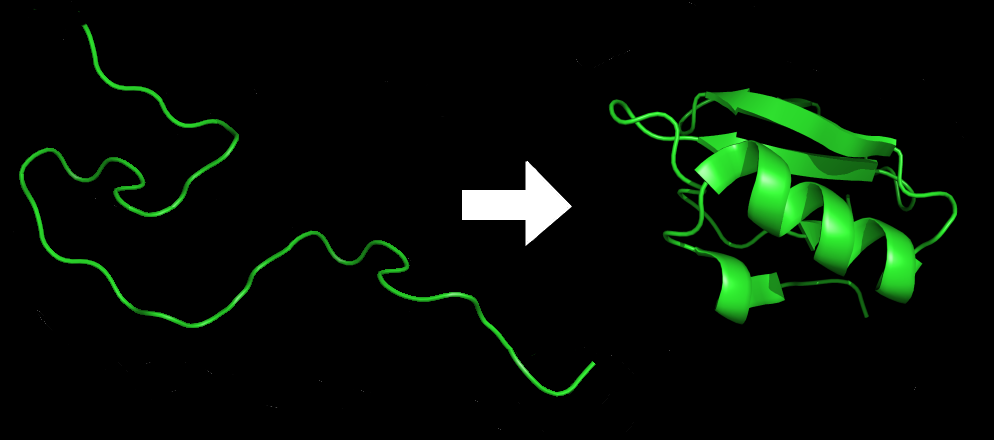
- For top scoring sequences, visualize predict homology structure with tools such as Swiss Model.
2. Learning Problem
 Designing novel protein structures is important both for
protein-based drug development and genetic engineering. We created a generative model that produces
sequences with one or more structural properties (see Experiments).
Designing novel protein structures is important both for
protein-based drug development and genetic engineering. We created a generative model that produces
sequences with one or more structural properties (see Experiments).
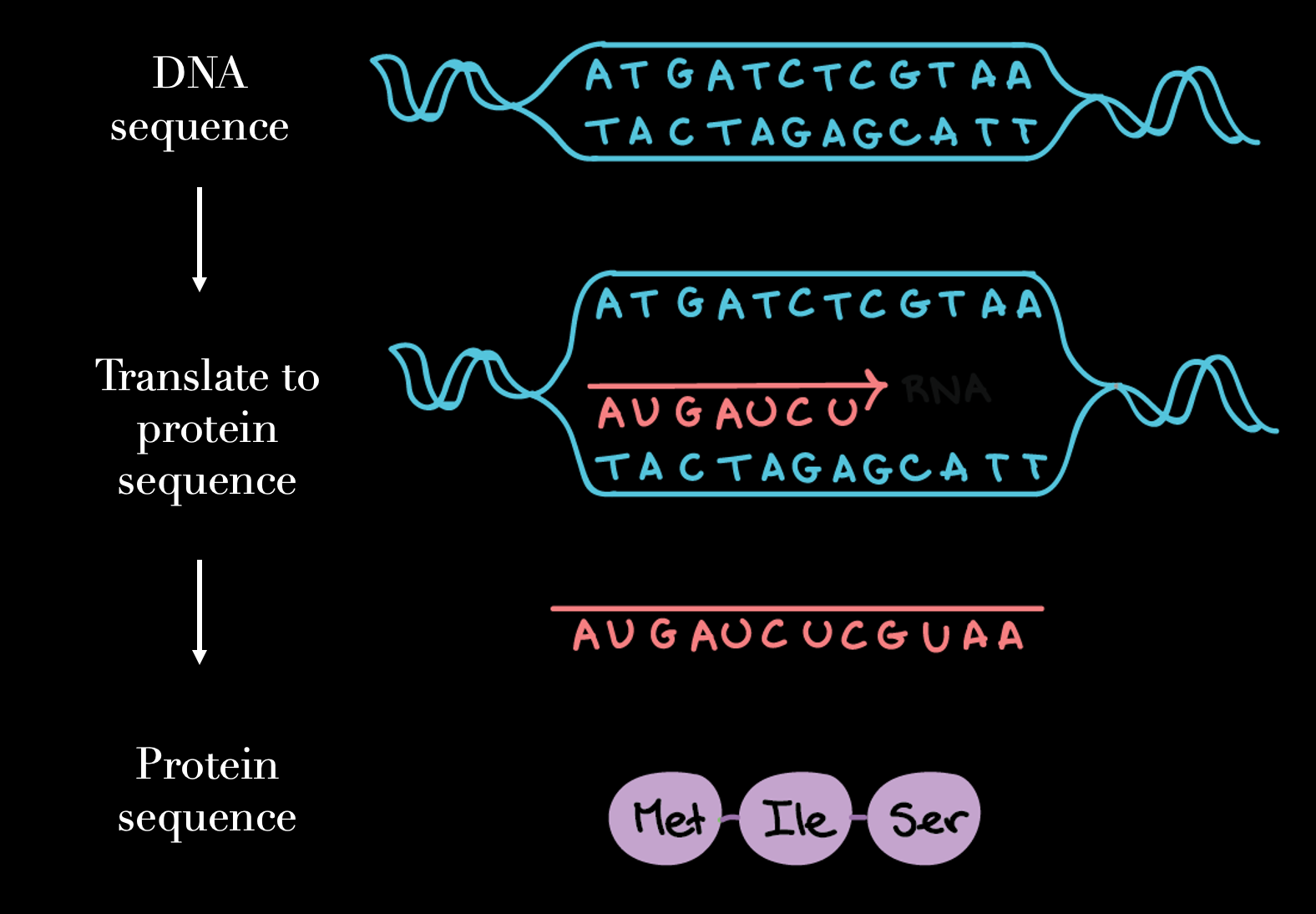
Protein sequences consist of 20 possible amino acids, each
determined by a triplet of 4 possible DNA letters (A, T, C, G). For example an amino-acid
lysin (letter code L) is coded as AAG in the DNA code. We have used this property to
to reduce the complexity of the problem - instead of learning 20 character, it suffices to learn
only 4, and trained the model to produce valid DNA sequences. These are then translated into the
protein sequence.
The translation is deterministic and one-to-one *. Thus, it is possible to go back and forth between DNA and protein
sequences to lower the computational expenses.
(*with a few expections that are not-siginificant for this task)
Structural properties of protein sequences
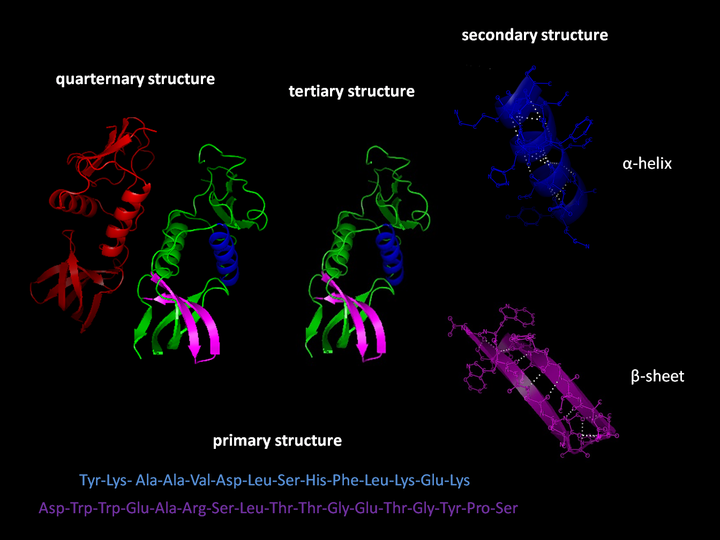 Our model produces sequences that are predicted to contain specific secondary structures. There are
8 recognized secondary protein structures, with associated letter codes.
Formally, the problem of predicting these structures from sequences is called the Q8-problem.
Our model produces sequences that are predicted to contain specific secondary structures. There are
8 recognized secondary protein structures, with associated letter codes.
Formally, the problem of predicting these structures from sequences is called the Q8-problem.
- helix (G)
- α-helix (H)
- π-helix (I)
- β-stand (E)
- bridge (B)
- turn (T)
- bend (S)
- coil (C)
Previous work on topic of feature optimization (Gupta et al. 2019) focused on optimizing for one structure - alpha helices (H). However, as discovered during exploratory data analysis, this state is extremely common in proteins and, thus, is less challenging to optimize for. In this work we extended the approach to other structures and to optimize for multiple combinations of different structures at the same time.
3. Feedback Net Architecture
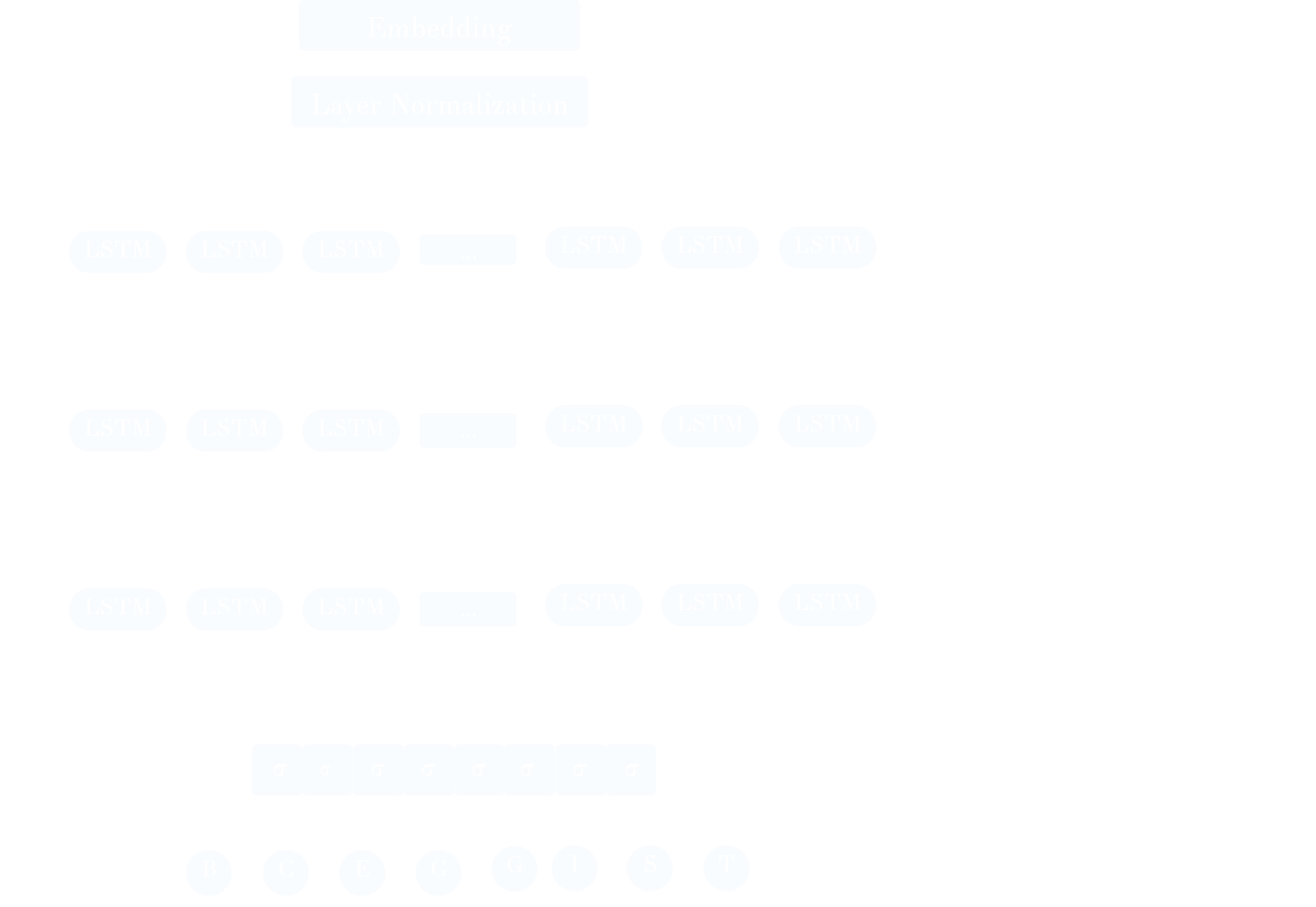 Given the sequence, language-like, nature of the problem we went with architecture that combines an embedding layer and bidirectional LSTMs.
We started by optimizing network as a single-label task. However, this approach appeared to be non-suitable for our problem, as we later learned that dataset is dominated by 3 labels. we decided to focus on metrics like precision and recall,as they best describe sensitivity to underrepresented labels.
Thus, we shifted approach to a multi-label classifier. More specifically, the last layer of the network consists of eight nodes, each with sigmoid activation and the network utilizes a binary cross-entropy loss. Thus, given encoded sequence input, feedback outputs probability of 8 structural labels.
Given the sequence, language-like, nature of the problem we went with architecture that combines an embedding layer and bidirectional LSTMs.
We started by optimizing network as a single-label task. However, this approach appeared to be non-suitable for our problem, as we later learned that dataset is dominated by 3 labels. we decided to focus on metrics like precision and recall,as they best describe sensitivity to underrepresented labels.
Thus, we shifted approach to a multi-label classifier. More specifically, the last layer of the network consists of eight nodes, each with sigmoid activation and the network utilizes a binary cross-entropy loss. Thus, given encoded sequence input, feedback outputs probability of 8 structural labels.
4. GAN Architecture
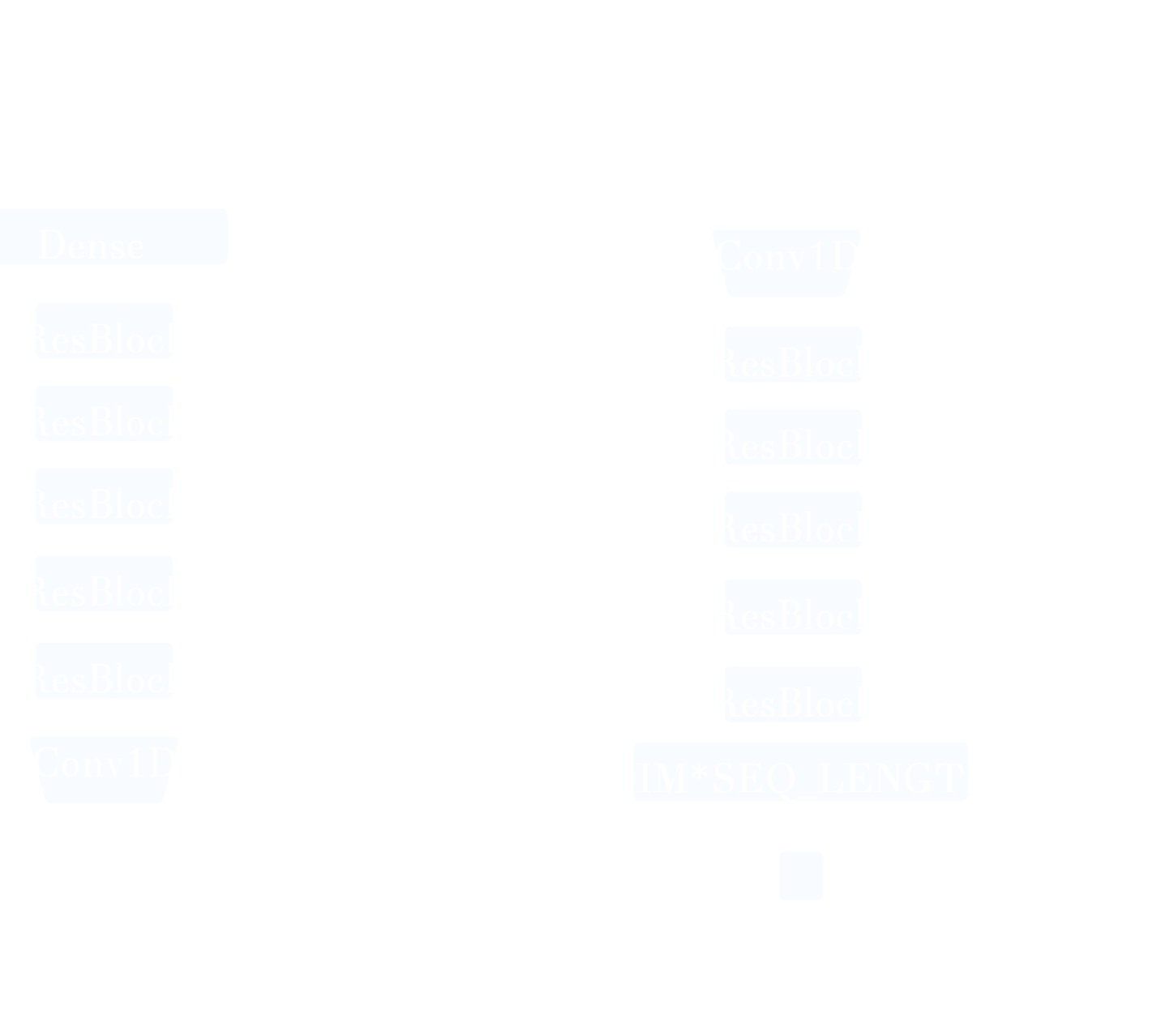 The architecture of the generative network was adapted from Gulrajani et al. 2017
and Gupta et al. 2019. The architecture is designed for language models and other sequences.
It consists of five Residual Blocks that perform 1D convolution operations and upsampling in the generator followed by downsampling in the discriminator.
The Wasserstein loss coupled with gradient penalty ensure stability of the model and enforce a Lipschitz constraint on the discriminator.
The architecture of the generative network was adapted from Gulrajani et al. 2017
and Gupta et al. 2019. The architecture is designed for language models and other sequences.
It consists of five Residual Blocks that perform 1D convolution operations and upsampling in the generator followed by downsampling in the discriminator.
The Wasserstein loss coupled with gradient penalty ensure stability of the model and enforce a Lipschitz constraint on the discriminator.